[코딩테스트] 프로그래머스 javascript 1단계 - 2016년, 소수 찾기
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
2016년
문제 설명
2016년 1월 1일은 금요일입니다. 2016년 a월 b일은 무슨 요일일까요? 두 수 a ,b를 입력받아 2016년 a월 b일이 무슨 요일인지 리턴하는 함수, solution을 완성하세요. 요일의 이름은 일요일부터 토요일까지 각 각 SUN,MON,TUE,WED,THU,FRI,SAT입니다. 예를 들어 a=5, b=24라면 5월 24일은 화요일이므로 문자열 "TUE"를 반환하세요.
이 문제로 약 20분가량을 헤맸다.
시간이 꽤나 걸린 이유는 Date 객체에 Month를 설정할 때 1을 빼줘야 한다는 사실을 기억하지 못했기 때문이다.
function solution(a, b) {
return new Date(2016,a-1,b).toString().slice(0,3).toUpperCase()
}
반드시 Date 객체에 월 -1 을 해야 한다.
또한 Date 객체를 string으로 전환해서 앞에 3글자를 가져올 수 있다.
const date = new Date().toString()
console.log(date)
//'Tue Jan 31 2023 15:19:04 GMT+0900 (한국 표준시)'
소수 찾기
문제 설명
1부터 입력받은 숫자 n 사이에 있는 소수의 개수를 반환하는 함수, solution을 만들어 보세요.
소수는 1과 자기 자신으로만 나누어지는 수를 의미합니다.
(1은 소수가 아닙니다.)
<문제 >
이 문제는 문제를 해결해결은 쉽지만 시간 복잡도를 생갹해야 하기 때문에 오래 걸렸다.
- 조건 : n은 2이상 1000000이하의 자연수입니다.
조건에서 변수 n이 100만개이기 때문에 2억개 미만이 되어야 하기 때문에
O(n**n)까지 가능하다.
따라서, 소수 판별 함수를 생성해서 매번 수를 계산하면 시간 초과가 일어난다.
해결 방법
소수 찾기 : 에라토스테네스의 체를 사용한다.
에라토스테네스의 체는 아래 gif 파일을 보면 이해하기 쉽다.
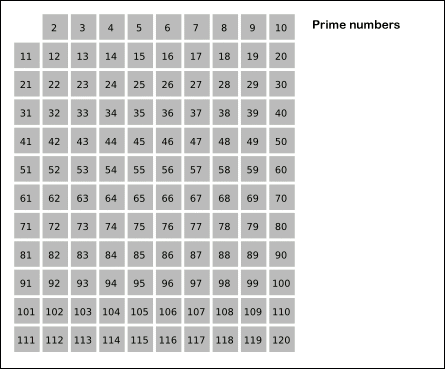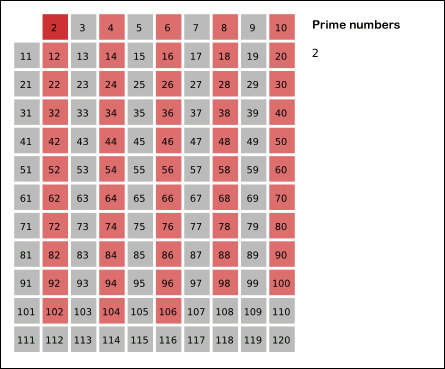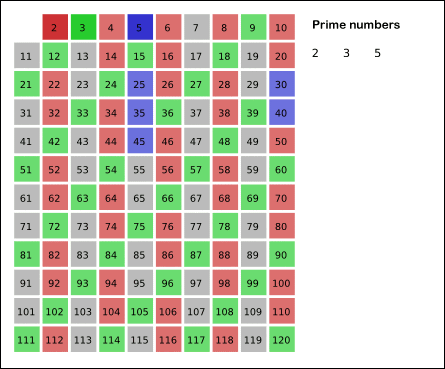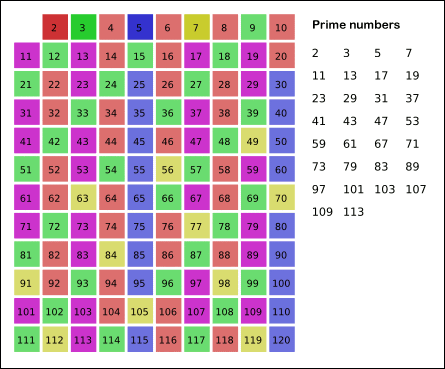
위 파일처럼 소수를 찾고 그 소수의 배수를 제거하는 것이다.
즉, set으로 2부터 n까지 넣고 배수들을 하나씩 제거하면 된다.
코드 풀이
1. set에 2~n까지 넣는다.
let set = new Set();
for(let i =2; i<=n;i++) {
set.add(i)
}
2. for문을 돌면서 소수의 배수를 제거한다.
- i의 배수들을 찾을 예정이므로 Math.sqrt(n)보다 같거나 작은 수까지만 반복 실행한다.
for(let i=2;i<=Math.sqrt(n);i++) {
if (set.has(i) {
for (let k = i*2; k<=n;k+=i) {
set.delete(k);
}
}
}
3. set의 크기를 출력한다.
return set.size
최종 코드
function solution(n) {
let prime = new Set()
if (n>=2) prime.add(2)
//짝수 제외 for문
for (let i = 3;i<=n;i+=2) {
prime.add(i)
}
// n의 배수를 prime에서 제거
for (let i =3; i<=Math.sqrt(n);i++) {
if (prime.has(i)) {
for (let j=i*2;j<=n;j+=i) {
prime.delete(j)
}
}
}
return prime.size
}